[study] Stanford CS224N: Lecture 3 - Backprop and Neural Networks

Week 3 task of Stanford CS244n: Natural Language Processing with Deep Learning

Lecture

Named Entity Recognition (NER)

Named Entity Recognition identifies and classifies named entities
into predefined entity categories such as person names, organizations…

For example,

“Harry Kane missed his penalty at the World Cup 2022.”

“Harry Kane” - (Person Name)
“World Cup 2022” - (Location)

Binary Word Window Classification

Binary Word Window Classification classifies center word
for each class based on the presence of word in a given context window.

The classification is binary because it classifies text into {yes/no}
given the {presence/absence} of the target word.

For Example,

“Heungmin Son scored a Hat-trick last week.” (target word -> “Hat-trick”)

The classification will classify the presence of the target word “Hat-trick” in the sentence.
Label $1$ if “Hat-trick” is present in the sentence. If not, label $0$.

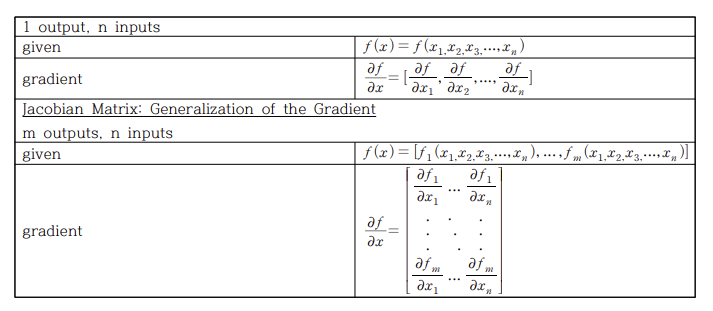
Matrix Calculus

Why Calculate gradients using matrix calculus?

1. Faster calculation speed than non-vectorized gradients
2. Is an effective method to handle similar iterative operations

Jacobian Matrix is a $mxn$ matrix of partial derivatives.

$n$ = inputs, $m$ = outputs, $f : R^n -> R^m$

Procedures

$x$ = input
$z = Wx + b$

Input Layer

$\frac{\partial z}{\partial x} = W$

Hidden Layer

$\frac{\partial h}{\partial z} = diag(f’(z))$

Output Layer

$\frac{\partial s}{\partial h} = u^T$

Jacobian Matrix

$\frac{\partial s}{\partial u} = h^T$

$\frac{\partial s}{\partial W} = \frac{\partial s}{\partial h}\frac{\partial h}{\partial z}\frac{\partial z}{\partial W}$

$\frac{\partial s}{\partial b} = \frac{\partial s}{\partial h}\frac{\partial h}{\partial z}\frac{\partial z}{\partial b}$

$\frac{\partial s}{\partial h}\frac{\partial h}{\partial z} = \delta$

$\frac{\partial s}{\partial b} = u^Tdiag(f’(z))I$

$\frac{\partial s}{\partial W} = \delta^Tx^T$

Back Propagation

Backpropagation reuses the weights of the network to update weights
to the direction of reducing the loss.

Backpropagation steps

1. Feed forward input x through the network to produce $\hat{y}$
2. Calculate difference between output $\hat{y}$ and target $y$
3. Backpropagate the derivative of loss function with $\hat{y}$
4. Backpropagate the derivative of $\hat{y}$ with hidden layer
5. Calculate the product of the gradients from 3 and 4
6. Update weights to the negative direction