[study] Stanford CS224N: Lecture 2 - Neural Classifiers - Lecture Review

Week 2 task of Stanford CS244n: Natural Language Processing with Deep Learning

Lecture (강의 내용)

Gradient Descent

$\theta^{new} = \theta^{old} - \alpha\nabla_{\theta}J(\theta)$

Gradient Descent calculates the gradient (slope) of the cost function,
which is the error between the predicted value and the actual value,
and updates $\theta$ to negative gradient to reach the minimum value.

However, since Gradient Descent calculates from a whole Dataset,
It costs too much memory and is time-consuming.

$\nabla_{\theta}J(\theta)$ = $\left[\begin{array}{clr} 0 \ … \ \nabla_{t} \ 0 \ \nabla_{\theta} \end{array}\right]$

Stochastic Gradient Descent (SGD) solves this problem by
updating the model parameters by using only one randomly selected training sample
in each iteration instead of using a whole Dataset.

However, SGD method also suffers similar problem from sparsity
since it derives gradient using one-hot vectors which requires a plethora of zero vectors.

Skip-gram uses a Negative Sampling method to solve this problem.

Negative Sampling

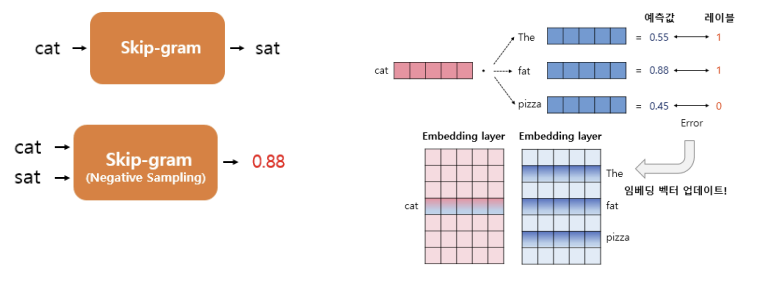
Negative Sampling trains binary logistic regressions for a true pair versus several noise pairs.

Negative Sampling inputs both center word and context word,
and predicts a probability of these two words actually present
in a certain window size.

After making several predictions for center word and context words,
The model updates from the error between the predicted value and the actual value
using the backpropagation.

Co-occurrence Matrix

SVD (Singular Value Decomposition)

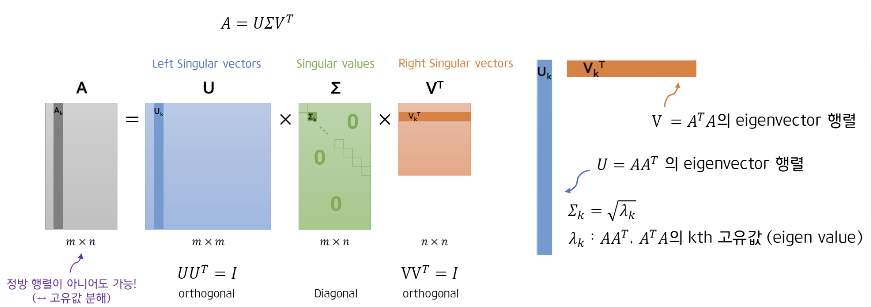
$A = U\Sigma{V}^T$

$A : m x n$ rectangular matrix
$U : m x m$ orthogonal matrix
$\Sigma : m x n$ diagonal matrix
$V : n x n$ orthogonal matrix

Singular Value Decomposition reduces the dimensionality of the data but preserves the most important aspects of the data.

1. Compute the left and right eigenvectors of matric $A$, which is $U_k$ and $V_k$.
2. The singular values of A are the non-negative square roots of the eigenvalues of the matrix $A^{T}A$. Arrange them at $\Sigma$.
3. The product of $U$, $\Sigma$, $V$ is the original matrix $A$.