[nlp_paper] attention Paper Review

DSL 논문 스터디 6기 손예진님이 발제하신 내용을 기반으로 작성했습니다.

Introduction

As mentioned prior, Seq2seq neural network model suffers huge information loss since it summerizes all its information into one single context vector.
Especially, if a train sequence is lengthy, the Seq2seq model was not able to translate it fluently.
Attention model solves this problem by introducing alignment with translation.

Model Architecture

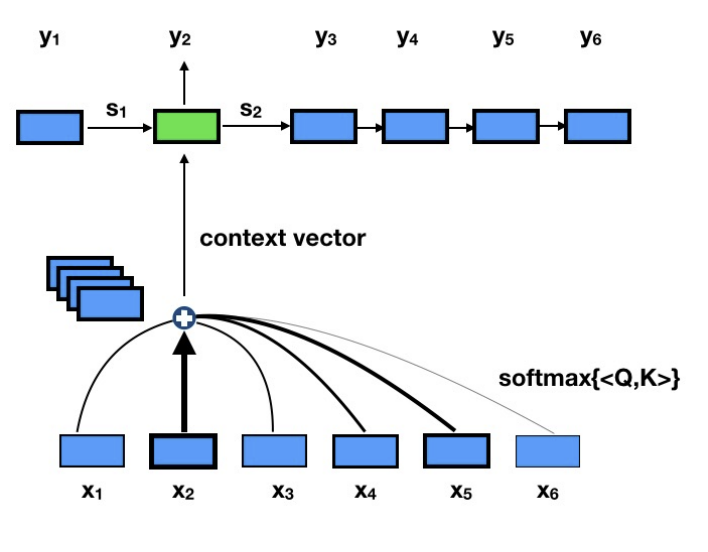
Instead of Seq2seq model summerizing all information from its Src sentences into one single context vector,
Attention model “attends” to a particular part of src sentences when making every predictions.

Paper Review

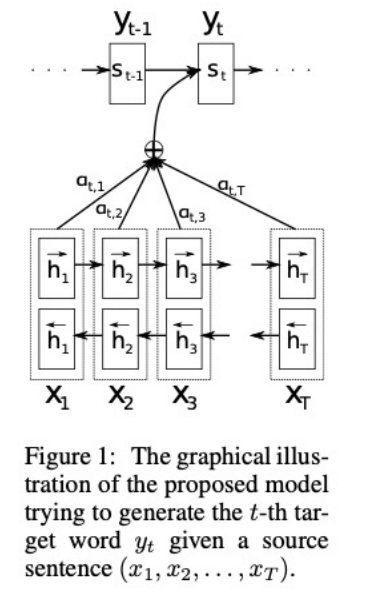
The Attention model works by a specific attention mechanism “Scaled Dot Product Attention”

$Attention(Q, K, V) = softmax(\frac{QK^T}{\sqrt(d_k)})$

Attention mechanism splits the input into three categories:

($Q$) for query (hidden-state at t-1 decoder cell)
($K$) for key (hidden-state at every encoder cell)
($V$) for value

By calculating the Dot product of query $Q$ and key $K$, and scaling it by the square root of key $k$’s dimension,
The attention mechanism produce a score for each key value pair that indicates the importance of value $v$.

By computing scores for each value $v$, the Attention model is able to decide a particular important part of the src sentences it should attend to when making every predictions.

Prediction Procedures

$1$. Get Attention Score for every decoder hidden state $s_{t-1}$ and encoder hidden state $h_i$

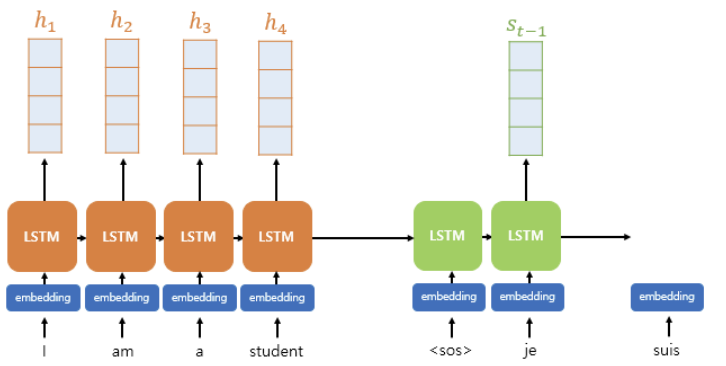
Consider a depth-4 attention translation model.

When predicting for $s_t$, first get an Attention Score from decoder hidden state $s_{t-1}$ and encoder hidden state $h_i$.

$score(s_{t-1}, h_i) = e^t = {W_a}^Ttanh(W_{b}s_{t-1} + W_{c}h_{i})$

where $W_a$, $W_b$, $W_c$ is a trainable weight vectors.

$2$. Use a softmax function to compute Attention Distribution

By applying a softmax function to attention score $e^t$, get a probability distribution that sums up to 1.

$3$. Sum up every Attention Weight and hidden-state to compute Attention Value (context vector)

$4$. Compute $s_t$ from Attention Value

$5$. Predict next value $v$ from the hidden state $s_t$

Results

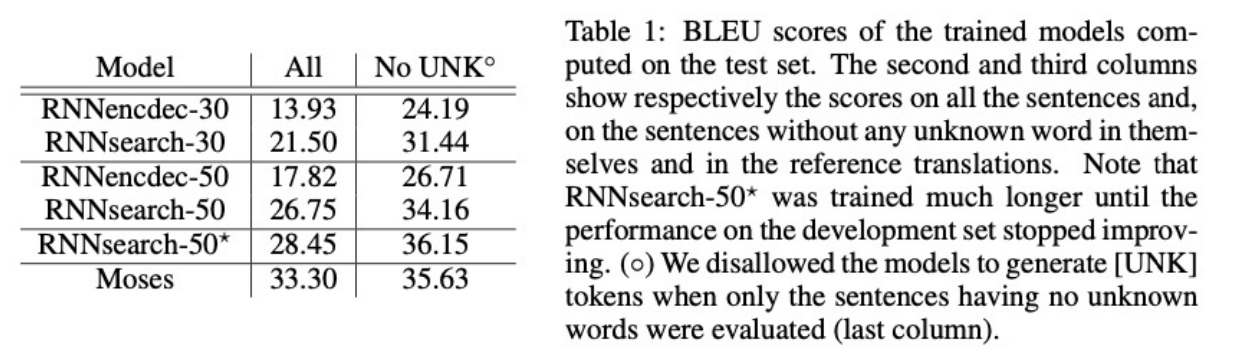
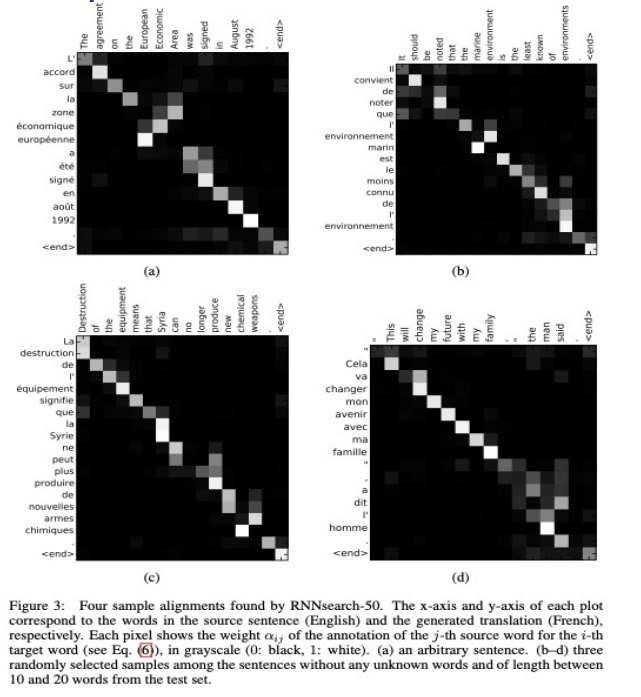
1. Attention model (seqseq + attention) was able to surpass BLEU score of Seq2seq model in every instances.

2. Attention model was able to surpass Moses(= Traditional SMT) despite trained from limited vocab sources.

3. Since Attention model was trained with a “soft alignment”, it is able to translate more fluently by relating to more similar vocabs.

4. By making context vector from the particular part of src sentences the Attention model was able to solve information loss from summerizing all information in a seq2seq model.