[Machine Learning] Support Vector Machine

Skim through fundamental machine learning concepts and mathematical implications.

Support Vector Machine

Support Vector Machine maximizes the margin between each class data by solving for a hyperplane.

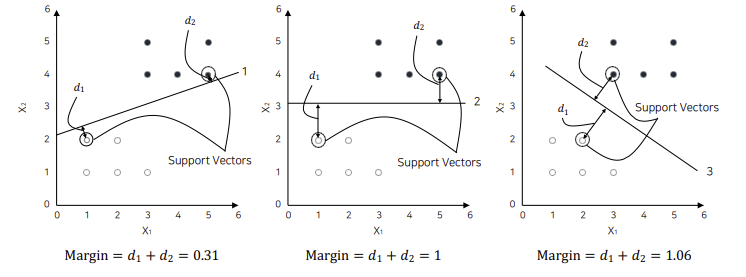
Support Vector = The closest class data from the hyperplane
Margin = Sum of minimum distance of support vectors and the hyperplane.

Constraints

Hyperplane : $f(X) = w_0 + w_1X_1 + w_2X_2 + … + w_pX_p$

Objective Function: $Max.M(margin)$

Constraints:

1. Most of the data should be further away from the hyperplane than the support vector.
2. Allow some data to become closer to hyperplane than the support vector.

Slack Variable $\xi$ allows misclassified data to make model more robust to an outlier.

$\xi \ge 0$

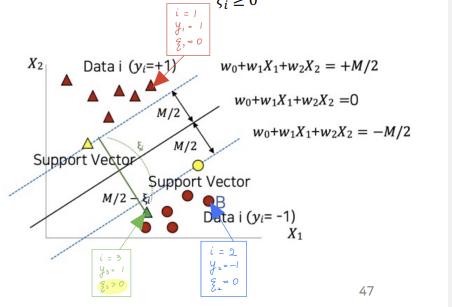
The ideal hyperplane = $w_0 + w_1X_1 + w_2X_2 = 0$

vectors located higher than the hyperplane : $w_0 + w_1X_1 + w_2X_2 >= +M/2$
vectors located lower than the hyperplane : $w_0 + w_1X_1 + w_2X_2 <= -M/2$

1. $y_i(W \circ X_i + w_0) \ge M/2$
2. $y_i(W \circ X_i + w_0) \ge M/2 - \xi_i$

–>

$y_i(W \circ X_i + w_0) \ge M/2 - \xi_i$,
$\xi_i \ge 0$

–>

$y_i[(W \circ X_i) + w_0] \ge 1 - \xi_i ( i = 1, … , n)$,
$\xi \ge 0$

Objective Function

$Max M = Max\frac{2}{

W

} = Min\frac{

W

}{2} = Min\frac{(

W

)^2}{2}$

Objective Function : $Min\frac{(

W

)^2}{2} + C\Sigma_i\xi_i$

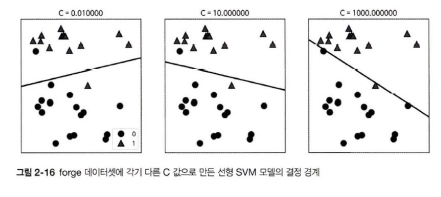
$C$ = Hyperparameter, the lower, the softer the model.

Hard Margin Classification: High $C$ value. Is sensitive to outliers. Soft Margin Classification: Low $C$ value. Classifies sample more flexible.

Non-Linear SVM

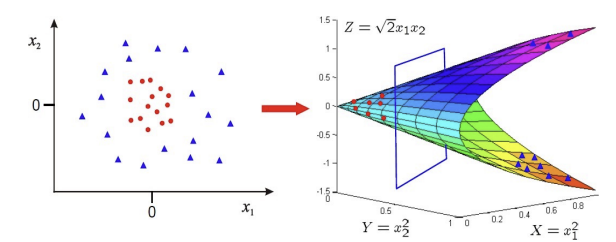
Non-Linear SVM Uses the kernel function to solve hyperplane from the different dimension.

Kernel Function

Kernel Function transforms the dimension of the input data to solve hyperplane from the different dimension.

$k(X_i, X_j) = \Phi(X_i)^T\Phi(X_j)$

Kernel Trick calculates the dot product of transformed input without actually transforming it.

Original method: Data -> Transform -> Dot Product
Kernel Trick: Data -> Skip -> Dot Product

Multiclass SVM

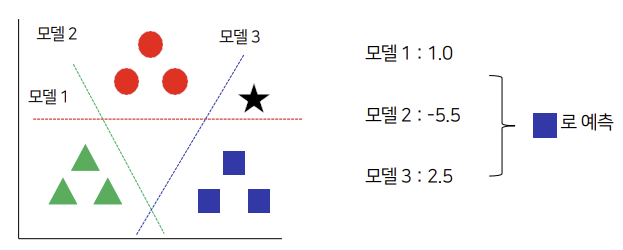
One-Versus-Rest model calculates output for each two combinations, and classifies data into the class with the highest output

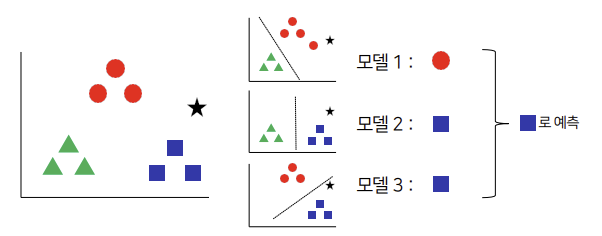
One-Versus_One model calculates output for each two combinations, and classifies data by majority voting method.