[Machine Learning] $R^2$ and Regularization

Skim through fundamental machine learning concepts and mathematical implications.

Importance of Scaling Data

Regression analysis is very sensitive at scaling data.
So, it is recommended to minimize influence if the input variables’
range and distribution is different.

Min-Max Scaling compares differences according to the rate of change.

Standard Scaling compares how much variables have changed throughout its distribution.

Correlation Coefficient $R^2$

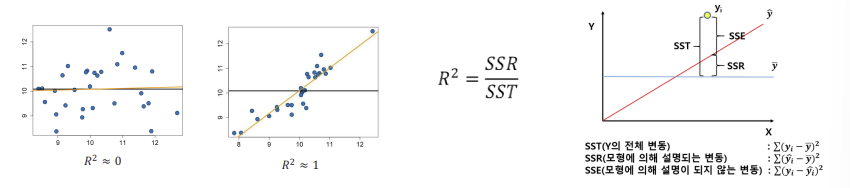
$R^2$ indicates how much a predicted value $\hat{Y}$ explains the actual value $Y$ than the mean value $\overline{Y}$.

$R^2$ has a range from $0$ to $1$, and the closer it gets to $1$, the powerful the regression model is.

Overfitting

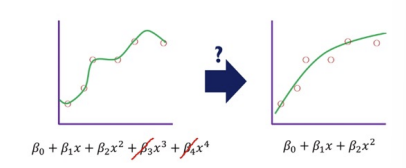
Overfitting is when a model is not general because it is overly fitted to the train data.

So it is recommended to use $R_{adj}^2$ , $R_{pred}^2$ to evaluate the efficiency of the model.

Adjusted $R^2$ $R_{adj}^2$ penalizes model by the number of input variables.

$R_{adj}^2 = 1 - \frac{SSE(n-1}{SST(n - p - 1)}$

Predicted $R^2$ $R_{pred}^2$ evaluates model from validation data.

$R_{pred}^2 = 1 - \frac{\Sigma_{i=1}^k(y_i - \hat{y}i)^2}{\Sigma{i=1}^k(y_i - \overline{y}_i)^2}$

If $R^2$ is much lesser than $R_{adj}^2$ and $R_{pred}^2$, the model is overfitted.

Variation Index Factor (VIF)

Variation Index Factor (VIF) evaluates multicollinearity between variables.
If the variables are highly correlated, the correlation coefficients become highly unstable.

$VIF_k = \frac{1}{1 - R_k^2}$

If $VIF \ge 10$, the variables have multicollinearity problem.

Regularization

Regularization removes the effect of negative input variables by adding constraint $f(\hat{\beta})$ to regression coefficients.

$min\Sigma_{i=1}^n(y_1 - \hat{y}_i)^2 + f(\hat{\beta})$

Ridge Regression

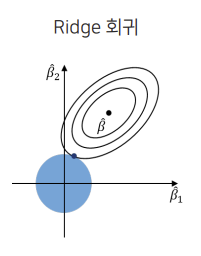
Ridge Regression (L2 Regularization) substitutes the sum of the squares of regression coefficients to contraint $f(\hat{\beta})$

($\lambda$ = hyperparameter makes more coeffients $0$ if higher)

$Minimize$ $ $ $min\Sigma_{i=1}^n(y_1 - \hat{y}i)^2 + \lambda\Sigma{i=1}^p\hat{\beta}_j^2$

Ridge reduces regression coeffients close to $0$.

LASSO

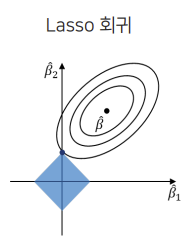
LASSO (L1 Regularization) substitutes the sum of the absolute values of regression coefficients to contraint $f(\hat{\beta})$

($\lambda$ = hyperparameter makes more coeffients $0$ if higher)

$Minimize$ $ $ $min\Sigma_{i=1}^n(y_1 - \hat{y}i)^2 + \lambda\Sigma{i=1}^p

\hat{\beta}_j

$

LASSO reduces regression coeffients to $0$.