[Machine Learning] Linear Regression and OLS

Skim through fundamental machine learning concepts and mathematical implications.

Supervised Learning:

Supervised Learning trains from a labeled input data to predict
the output data: $Y$ (Label)

Regression

Regression explores the relationship between variables.
It predicts continuous outcome and data.

Classification

Meanwhile, Classification predicts discrete figures from categorical data.
Classification is further classified into Binary Classificaion and Categorical Classification.

Linear Regression

If a data is supervised & continuous, use Regression to predict outputs.

Linear Regression models a linear correlation between
$X$ (Independent Variable) and $Y$ (Dependent Variable).

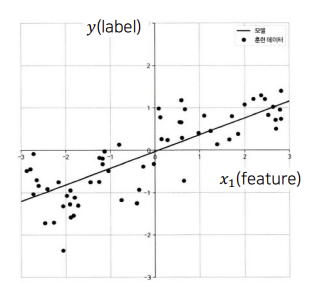
$X$ $(feature)$ : Independent Variable

Independent Variable affects other variables.

$Y$ $(label)$ : Dependent Variable

Dependent Variable is affected by other variables.

Simple Linear Regression

Simple Linear Regression predicts Dependent Variable from a single independent variable.

$\hat{y} = \beta_0 + \beta_1x_1$

Regression Coefficient represents an average change of output $Y$ when input $X$ is increased by $1$.

Regression Coefficient = $\beta_0$, $\beta_1$

Multiple Linear Regression

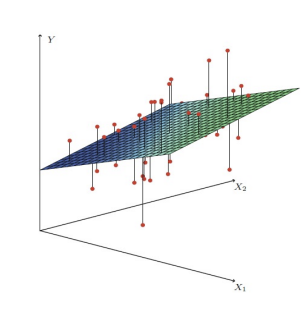
Multiple Linear Regression predicts dependent variable from multiple independent variables.

$\hat{y} = \beta_0 + \beta_1x_1 + … + \beta_kx_k$

Regression Coefficient = $\beta_0$, $\beta_1$, … , $\beta_k$

Ordinary Least Squares (OLS)

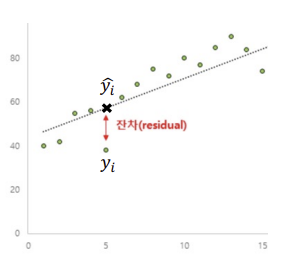
Residual : a difference between actual output and predicted output.

$e_i = y_i - \hat{y}_i$

Ordinary Least Squares estimates regression coefficients that minimizes the loss between the data and the regression,
Sum of Squared Errors (SSE)

$min \Sigma_{i=1}^n(y_i - \hat{y}_i)^2$

Proof.

$SSE$ $= \Sigma_{i=1}^n(y_i - \hat{y}i)^2$ $= \Sigma{i=1}^n(y_i - \hat{\beta}0 - \hat{\beta}_1x{i1} - … - \hat{\beta}kx{ik})^2$

$= (Y - X\beta)^T(Y - X\beta) = Y^TY - Y^T(X\beta) - (X\beta)^TY + (X\beta)^T(X\beta)$

$= Y^TY - 2\beta^TX^Ty + \beta^TX^TX\beta$

Do a Partial Derivative $\frac{\partial}{\partial \beta}$,

$\therefore \beta = (X^TX)^{-1}X^Ty$

So, $min \Sigma_{i=1}^n(y_i - \hat{y}_i)^2$ -> $\beta = (X^TX)^{-1}X^Ty$

Maximum Likelihood Estimation

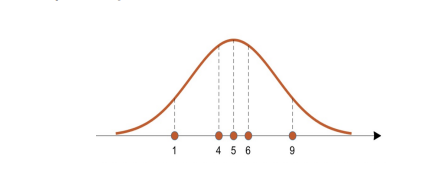
Likelihood represents a probability of a data made from a certain distribution.

To calculate all likelihoods of a data, calculate the height of all candidate distribution from each data sample and multiply them.
This is Maximum Likelihood Estimation (MLE).

Maximum Likelihood Estimation (MLE) finds the parameters of the distribution that maximizes the likelihood in the given situation.

likelihood function = $P(x

\theta) = \Pi P(x_k

\theta)$

Log-likelihood function = $\Sigma_{i=1}^n\frac{\partial}{\partial \theta}logP(x_i

\theta) = 0$