[Machine Learning] Decision Tree

Skim through fundamental machine learning concepts and mathematical implications.

Decision Tree

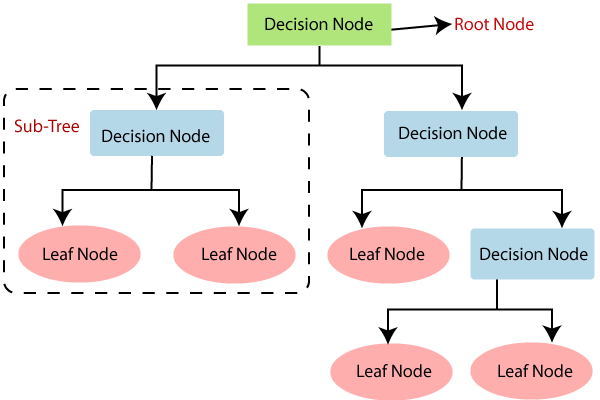
Decision Tree represents Decision Rules into a flowchart-like tree structures in order to maximize the categorization of class data.

Root Node represents the population of the data.

Branch represents an outcome of the decision rule,
predicts a categorical output from the given input data.

Decision node represents intermediate stage between Root node and the Leaf node.

Leaf node is the final subset of a decison tree.

Classification and Regression Tree (CART)

Decision Tree can be utilized for both classification and regression task.

Decision Tree trains to minimize impurity value.

Impurity : a measure of homoegeneity of the labels

Classification and Regression Tree (CART) utilizes Gini Impurity to judge splits and determine what predictor variable to use.

Gini Impurity

Gini Impurity represents the probability of randomly selecting an alternate class data.

$Gini(S) = \displaystyle \sum_{i=1}^c\displaystyle \sum_{i=1}p_ip_{i’} = $ $\displaystyle \sum_{i=1}^cp_i\displaystyle \sum_{i=1}p_{i’} = $ $\displaystyle \sum_{i=1}^cp_i(1 - p_i)$

$= 1 - \displaystyle \sum_{i=1}^c{p_i}^2$

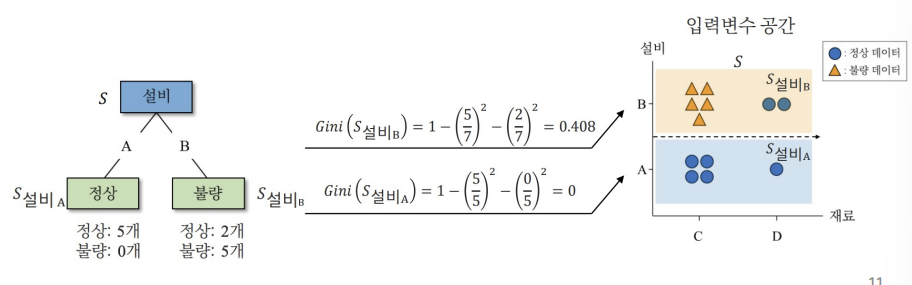
$Gini(S) = 1 - p_+^2 - p_-^2$

$S$ : Partitioned data set

$P+$ : percentage of ‘+’ labeled data

$P-$ : percentage of ‘-‘ labeled data

Information Gain

Information_Gain(S, A) represents the subtracted value of the impurity of the parent node from the impurity of the child nodes.

The split with the highest Information gain is chosen.

$Information Gain(S, A) = Gini(S) - \displaystyle \sum\frac{

S_v

}{

S

}Gini(S_v)$

$s.t.$

$Gini(S)$ = Impurity of the parent node

$\displaystyle \sum\frac{

S_v

}{

S

}Gini(S_v)$ = Impurity of child nodes.

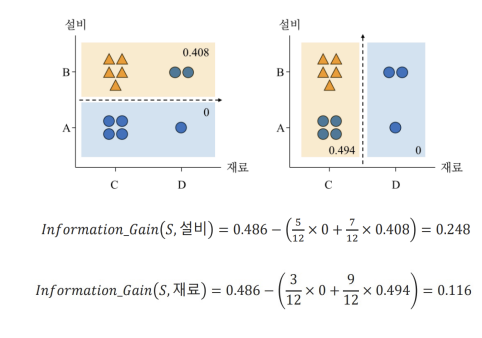
$0.248 \ge 0.116$

$Information Gain(S, 설비)$ $(0.248)$ is chosen.

Procedures

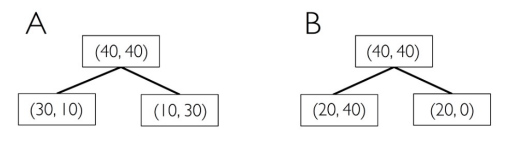
1. Gini Impurity

A

$I_G(D_p) = 1 - (\frac{40}{80}^2 + \frac{40}{80}^2) = 0.5$

$I_G(D_{left}) = 1 - \frac{30}{40}^2 - \frac{10}{40}^2 = \frac{3}{8} = 0.375$

$I_G(D_{right}) = 1 - \frac{10}{40}^2 - \frac{30}{40}^2 = \frac{3}{8} = 0.375$

$IG_A = 0.5 - \frac{40}{80} * 0.375 - \frac{40}{80} * 0.375 = 0.125$

B

$I_G(D_{left}) = 1 - \frac{20}{60}^2 - \frac{40}{60}^2 = \frac{4}{9} = 0.444$

$I_G(D_{right}) = 1 - \frac{20}{20}^2 = 0$

$IG_B = 0.5 - \frac{60}{80} * 0.444 - \frac{20}{80} * 0 = 0.166$

$\therefore A \le B$

Split B is chosen.

Pruning

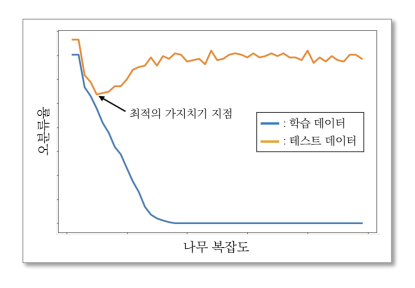
Pruning removes leaf nodes to prevent overfitting

pre-pruning : The decision tree stops branching if a certain condition is met (max_depth, min_sample_split)
post-pruning : converts insignificant subtrees to leaf nodes after the tree is completed.

Cost-Complexity Pruning

Cost-Complexity Pruning (CCP) splits node into child nodes when the imprity of the model is imrpoved.

$CC(T) = Err(T) + \alpha

T

$

$CC(T)$ : cost-complex variable of the decision tree

$Err(T)$ : misclassification rate of validation data

$

T

$ : # of leaf nodes

$\alpha$ : hyperparameter (lower -> robust)

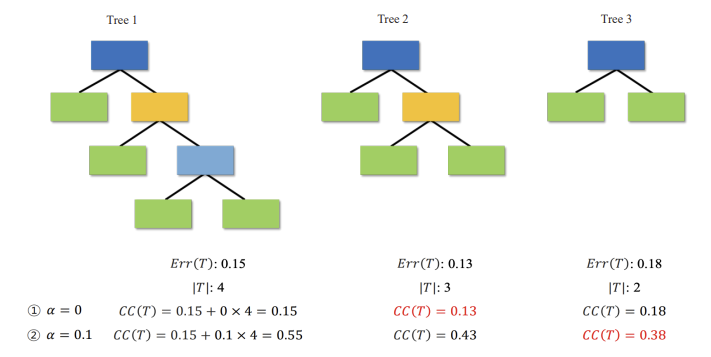
$0.15 \ge 0.13 \le 0.18$
$0.55 \ge 0.43 \le 0.38$

$\therefore$ decion tree 2 is the best option.